Calculul Modulului caderii de tensiune

Calculul modulului caderii de tensiune depinde de tipul retelei electrice respectiv, de regimul de incarcare al acesteia.

Admitand ca reteaua electrica este echilibrata, caderile de tensiune intr-un sistem electric trifazat pot reprezenta :

- un sistem electric trifazat simetric, daca sistemul de curenti trifazati de sarcina este simetric;

- un sistem electric trifazat nesimetric, daca sistemul de curenti trifazati de sarcma este nesimetric. In acest caz, se va calcula caderea de tensiune pe faza cea mai incarcata.

A.1 Calculul pierderilor de tensiune in retele electrice incarcate simetric.

A.1.1- cu o sarcina concentrata la capat.

In fig. 12.2. se prezinta schema electrica corespunzatoare acestui caz.

Adoptand ca referinta tensiunea de faza la receptor, Ur, fig.12.2.b, rezulta:

(12.11)

respectiv:

deoarece in retele incarcate simetric (pentru alimentarea receptorilor trifazati de forta) curentul pe nul este zero :

(12.12)

iar conductorul de nul nici nu exista.

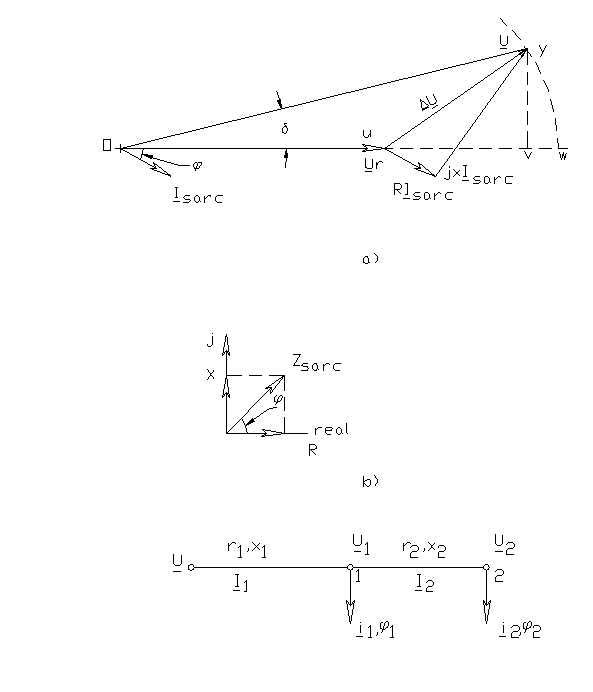
Diagrama fazoriala corespunzatoare fig.12.2.b. este prezentata in fig.12.3.a., unde s-a considerat RE prin impedanta: Z=R+jX iar impedanta :

Modulul caderii de tensiune ,ΔU, , este segmentul uw, adoptand ca referinta tensiunea la receptor. Rezulta:

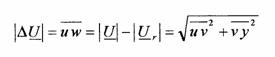
Determinarea analitica a valorii acestui modul este posibila, dar dificil de efectuat. Deoarece, corespunzator valorilor admise ale caderilor de tensiune unghiul δ , dintre U si U_r ,are valori foarte mici,(2÷4)⁰ electrice, se admite aproximarea

Ca urmare, valoarea modulului caderii de tensiune se determina ca proiectia componentelor acesteia pe directia axei de referinta (U_r). Aceasta valoare este definita in literatura de specialitate drept pierdere de tensiune, iar modulul caderilor de tensiune se vor calcula ca pierderi de tensiune.

Rezulta, pentru pierderea de tensiune pe faza unei retele electrice trifazate simetrice, expresia analitica:

Deoarece in practica se opereaza cu puterile trifazate, iar verificarile se efectueaza cu valorile procentuale, expresia (12.15) se poate transforma astfel:

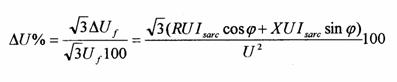
respectiv:

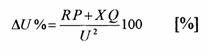
unde: -P si Q sunt puterile trifazate, activa si reactiva, absorbite de sarcina concentrata la capat.

AL2. - cu doua sarcini concentrate .

Cu i₁ si i₂ s-au notat curentii celor doua sarcini concentrate, iar φ₁ si φ₂ reprezinta defazajul dintre acesti curenti si tensiunile care ii determina, U₁ si U₂; cu r si x s-au notat parametrii unui tronson al retelei.

Curentii pe tronsoanele retelei ,care determina caderile de tensiune, determinati de cei de sarcina sunt,

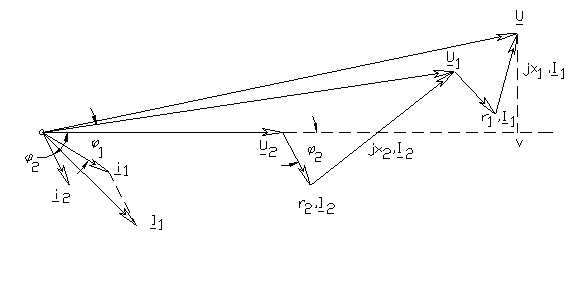
Pentru a calcula pierderea de tensiune intre U₁ si U₂ , ca suma a pierderilor de tensiune corespunzatoare caderilor de tensiune :

si adoptand ca referinta pe U₂, sunt necesare urmatoarele aproximari :

-proiectia fazorului r₁I₁ pe directia lui U₂ se aproximeaza cu r₁I₁cosφ₁ , desi unghiul real nu este φ₁ ci unghiul dintre I₁si U₂ .

-in mod similar proiectia fazorului x₁I₁ pe directia lui U₂ se aproximeaza cu x₁I₁sinφ₁.

Ca urmare, pierderea de tensiune in retele electrice trifazate incarcate simetric cu doua sarcini concentrate are expresia analitica :

In cazul mai multor sarcini concentrate este admisa aceeasi aproximatie, deoarece eroarea de unghi cumulata nu depaseste valoarea unghiului δ mentionata mai sus.

Deoarece in practica se cunosc valorile curentilor absorbiti de sarcini (i₁, i₂.i_n) expresia se poate transforma, notand :

care reprezinta rezistenta respectiv, reactanta de la sursa pana la sarcina concentrata astfel:

iar daca se opereaza cu puterile trifazate ale sarcinilor (p_i,q_i):

[%]

A.2. Calculul pierderilor de tensiune in retele electrice trifazate incarcate nesimetric.

Retelele electrice trifazate care alimenteaza si receptori monofazati (corpuri de iluminat si prize), pe de o parte ,au conductor de nul iar ,pe de alta parte, pe acesta circula un curent determinat de rezultanta sumei vectoriale, fig.12.2.,:

Caderea totala de tensiune pentru o faza va avea doua componente :

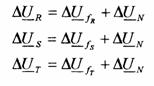
unde:

- DU_FRST este caderea de tensiune pe conductorul de faza si care se calculeaza asa cum s-a aratat anterior ;

- DU_N=I_N(R_N+jX_N) – este caderea de tensiune pe conductorul de nul care, in principiu, se calculeaza similar cu cea de pe conductorul de faza , daca se cunosc valorile curentului I_N.

Deoarece caderea de tensiune totala este suma a doua marimi vectoriale, este dificila determinarea valorii modulului acesteia si a valorii procentuale necesare verificarilor.

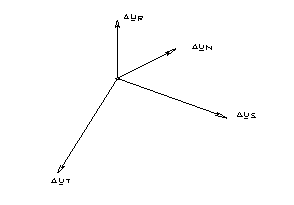
Totodata, caderile de tensiune pentru cele trei faze sunt diferite din doua cauze :

- pe de o parte, curentii pe faze sunt diferiti:

- pe de alta parte, caderea de tensiune pe nul este unica, iar caderile de tensiune pe conductoare de faze formeaza un sistem electric trifazat.

Pentru calculele de verificare este necesar sa se determine modulul caderii de tensiune totala pentru circuitul de faza cel mai incarcat.

Analitic se demonstreaza ca, rezultanta sumei vectoriale a vectorilor ce formeaza un sistem trifazat are defazajul (directia si sensul) mai mic in raport cu vectorul cel mai mare dintre cei trei si ca urmare, valoarea cea mai mare a caderilor de tensiune se va inregistra pe faza cea mai incarcata. Deoarece calculul analitic riguros este laborios, in continuare se vor determina caderile de tensiune totale pentru un sistem electric trifazat nesimetric (cu patru conductoare) cu urmatoarele caracteristici particulare :

- curentul este cel mai mare pe faza R;

- sarcina are acelasi caracter pe fiecare faza, nesimetria fiind determinata de inegalitatea modulelor impedantelor de sarcina;

- se neglijeaza reactanta liniilor in raport cu rezistenta (admisa in retele electrice de joasa tensiune);

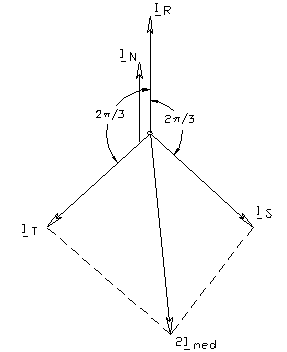
- sistemul de tensiuni este practic simetric. In aceste conditii particulare diagrama fazoriala a curentilor ,respectiv curentul pe conductorul de nul are expresia :

Adoptand ca referinta pe IR si inlocuind valorile curentilor Is si IT cu valoarea lor medie :

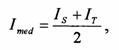
rezulta:

unde I_R/I_R este vectorul unitar de referinta, coliniar cu I_R.

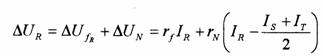
Ca urmare, in cazul particular considerat (curentul pe nul este in faza cu cel de pe faza cea mai incarcata, ceea ce permite determinarea caderii de tensiune totale pentru faza R ca suma algebrica a celor doua componente ,pierderea de tensiune va fi :

Determinarea pierderii de tensiune totale in mod similar si pe celelalte doua faze nu este corecta deoarece cele doua componente ale acesteia nu mai sunt coliniare (sunt defazate cu ± 2π/3).